Τύποι Κλασικής Γεωμετρίας

Γεωμετρικά σχήματα

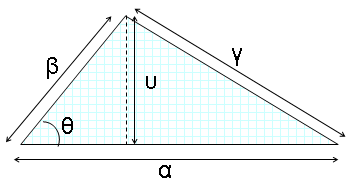
Τρίγωνο

Περίμετρος:

$\mathrm{\Pi }=\alpha +\beta +\gamma$

Εμβαδό:

$E=\frac{\alpha \upsilon }{2}=\frac{\alpha \beta \eta \mu \theta }{2}=\sqrt{s\left(\begin{array}{c}s-\alpha \end{array}\right)\left(\begin{array}{c}s-\beta \end{array}\right)\left(\begin{array}{c}s-\gamma \end{array}\right)}$ , όπου $s=\frac{\mathrm{\Pi }}{2}=\frac{\alpha +\beta +\gamma }{2}$ (ημιπερίμετρος)

• Στην περίπτωση ορθογωνίου τριγώνου είναι $\theta =90^o\Rightarrow \eta \mu \theta =1$. Άρα: β = υ και:

$E=\frac{\alpha \beta }{2}$.

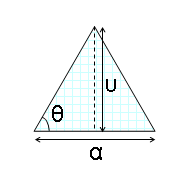
• Στην περίπτωση ισόπλευρου τριγώνου είναι: $\alpha =\beta =\gamma$, $\theta =60^o$ και $s=\frac{3}{2}\alpha$. Οπότε:

Περίμετρος:

$\mathrm{\Pi }=3\alpha$

Εμβαδό:

$E=\frac{\alpha \upsilon }{2}=\frac{{\alpha }^2\eta \mu 60^o}{2}=\frac{\sqrt{3}}{4}{\alpha }^2$

Το ίδιο προκύπτει και από τον άλλο τύπο:

$E=\sqrt{\frac{3}{2}\alpha {\left(\begin{array}{c}\frac{3}{2}\alpha -\alpha \end{array}\right)}^3}=\sqrt{\frac{3}{2}\alpha {\left(\begin{array}{c}\frac{1}{2}\alpha \end{array}\right)}^3}=\sqrt{\frac{3{\alpha }^4}{2^4}}=\frac{\sqrt{3}}{4}{\alpha }^2$

Ορθογώνιο παραλληλόγραμμο

Περίμετρος:

$\mathrm{\Pi }=2\left(\begin{array}{c}\alpha +\beta \end{array}\right)$

Εμβαδό:

$E=\alpha \beta$

Πλάγιο παραλληλόγραμμο

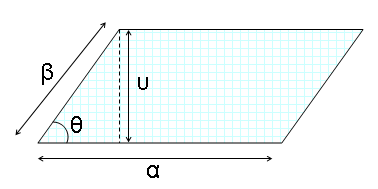
Περίμετρος:

$\mathrm{\Pi }=2\left(\begin{array}{c}\alpha +\beta \end{array}\right)$

Εμβαδό:

$E=\alpha \upsilon =\alpha \beta \eta \mu \theta$

Ρόμβος

Αρχείο:Rhombos.png

Περίμετρος:

$\mathrm{\Pi }=4\alpha$

Εμβαδό:

$E=\frac{{\delta }_1{\delta }_2}{2}$

Τετράγωνο

Αρχείο:Square1.png

Περίμετρος:

$\mathrm{\Pi }=4\alpha$

Εμβαδό:

$E={\alpha }^2$

Τραπέζιο

Αρχείο:Trapezium1.png

Περίμετρος:

$\mathrm{\Pi }=\alpha +\beta +\left(\begin{array}{c}\frac{1}{\eta \mu \theta }+\frac{1}{\eta \mu \varphi }\end{array}\right)\upsilon$

Εμβαδό:

$E=\frac{\alpha +\beta }{2}\upsilon$

Κανονικό πολύγωνο

1. Κανονικό πολύγωνο με n πλευρές και πλευρά α

Αρχείο:Hexagon1.png

Περίμετρος:

$\mathrm{\Pi }=n\alpha$

Εμβαδό:

$E=\frac{1}{4}n{\alpha }^2\sigma \varphi \frac{\pi }{n}=\frac{1}{4}n{\alpha }^2\frac{\sigma \upsilon \nu \frac{\pi }{n}}{\eta \mu \frac{\pi }{n}}$

2. Κανονικό πολύγωνο με n πλευρές εγγεγραμμένο σε κύκλο ακτίνας r

Περίμετρος:

$\mathrm{\Pi }=2\pi r\eta \mu \frac{\pi }{n}$

Εμβαδό:

$E=\frac{1}{2}\pi r^2\eta \mu \frac{2\pi }{n}$

Κύκλος

1. Κύκλος με ακτίνα r:

Περιφέρεια:

$\mathrm{\Pi }=2\pi r$

Εμβαδό:

$E=\pi r^2$

2. Τομέας κύκλου ακτίνας r, τόξου θ (σε ακτίνια, rad):

Αρχείο:Circpart.png

Μήκος τόξου:

$\mathrm{\Pi }=r\theta$

Εμβαδό:

$E=\frac{1}{2}{r}^2\theta$

3. Κύκλος ακτίνας r εγγεγραμμένος σε τρίγωνο με πλευρές α, β, γ:

Αρχείο:Circleintriangle.png

$r=\frac{\sqrt{s\left(\begin{array}{c}s-\alpha \end{array}\right)\left(\begin{array}{c}s-\beta \end{array}\right)\left(\begin{array}{c}s-\gamma \end{array}\right)}}{s}$
όπου $s=\frac{\mathrm{\Pi }}{2}=\frac{1}{2}\left(\begin{array}{c}\alpha +\beta +\gamma \end{array}\right)$

4. Κύκλος ακτίνας r περιγεγραμμένος σε τρίγωνο με πλευρές α, β, γ:

$r=\frac{\alpha \beta \gamma }{4\sqrt{s\left(\begin{array}{c}s-\alpha \end{array}\right)\left(\begin{array}{c}s-\beta \end{array}\right)\left(\begin{array}{c}s-\gamma \end{array}\right)}}$
όπου $s=\frac{\mathrm{\Pi }}{2}=\frac{1}{2}\left(\begin{array}{c}\alpha +\beta +\gamma \end{array}\right)$

• (Συνεχίζεται...)
• Επιστροφή στο Τμήμα Μαθηματικών