Πράξεις διανυσμάτων\Μέρος Β

Εσωτερικό γινόμενο

Το εσωτερικό γινόμενο είναι ένας πραγματικός αριθμός. Ο αριθμός αυτός είναι ανάλογος του μέτρου του κάθε διανύσματος, για παράδειγμα αν διπλασιαστεί το μέτρο του ενός διπλασιάζεται και το μέτρο του γινομένου. Επιπλέον, το εσωτερικό γινόμενο είναι το γινόμενο των μέτρων επί ένα δείκτη σχετικότητας κατευθύνσεων. Ο συντελεστής αυτός χαρακτηρίζει τη σχέση των κατευθύνσεων των δύο διανυσμάτων, ισούται με 1=+100%, αν τα διανύσματα είναι ομόρροπα, -1=-100% αν τα διανύσματα είναι αντίρροπα και με 0=0% αν τα διανύσματα είναι κάθετα, οπότε οι κατευθύνσεις είναι κατά κάποιο τρόπο ξένες μεταξύ τους.

Αυτός ο πολλαπλασιασμός δεν είναι κλειστή πράξη, δηλαδή το αποτέλεσμα δεν είναι του ίδιοιυ είδους με τα στοιχεία που συμμετείχαν αρχικά στην πράξη. Έτσι, δεν υπάρχει έννοια της προσεταιριστικής ιδιότητας. Οι περισσότερες ιδιότητές του προκύπτουν σε σχέση με άλλες πράξεις.

Για κάθε ζεύγος διανυσμάτων υπάχρουν δύο προβολές.

Ιδιότητες:

$\vec{α} \cdot \vec{β} = \vec{β} \cdot \vec{α}$

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Λύση
$\vec{α} \cdot \vec{β} = \| \vec{α} \| \| \vec{β} \| σ υ ν (\hat{\vec{α}, \vec{β}}) = \| \vec{β} \| \| \vec{α} \| σ υ ν (\hat{\vec{α}, \vec{β}}) = \vec{β} \cdot \vec{α}$

$\vec{α} \cdot (\vec{β} + \vec{γ}) = \vec{α} \cdot \vec{β} + \vec{α} \cdot \vec{γ}$

Άρα και

(\vec{β} + \vec{γ}) \cdot \vec{α} = \vec{β} \cdot \vec{α} + \vec{γ} \cdot \vec{α}

$λ (\vec{α} \cdot \vec{β}) = (λ \vec{α}) \cdot \vec{β}$

Καθετότητα

Δύο μη μηδενικά διανύσματα $\vec{α}$ , $\vec{β}$ είναι κάθετα αν και μόνο αν $\vec{α} \cdot \vec{β} = 0$ .

Άσκηση: Αποδείξτε τη συνθήκη καθετότητας
Λύση
Από τον ορισμό του εσωτερικού γινομένου για μη μηδενικά διανύσματα προκύπτει ότι δύο διανύσματα έχουν εσωτερικό γινόμενο μηδέν αν και μόνο αν η μεταξύ τους γωνία είναι ορθή, δηλαδή είναι μεταξύ τους κάθετα.

Ισχύει η ισοδυναμία: $\vec{α} \cdot \vec{β} = 0 \Leftrightarrow \vec{α} = \vec{0} \overset{´}{η} \vec{β} = \vec{0} \overset{´}{η}$ τα δύο διανύσματα είναι κάθετα μεταξύ τους.

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Λύση
Δύο διανύσματα είναι και τα δύο μηδενικά ή δεν είναι και τα δύο μηδενικά. Αν δεν είναι και τα δύο μηδενικά τότε ισχύει η συνθήκη καθετότητας, αλλιώς τουλάχιστον ένα είναι το μηδενικό διάνυσμα.

Ενναλλακτική απόδειξη (με χρήση της προβολής)
Λύση
Η προβολή του διανύσματος είναι το μηδενικό διάνυσμα, δηλαδή ταυτίζονται το πέρας και η αρχή του, άρα εξ' ορισμού της προβολής τα δύο διανύσματα είναι κάθετα μεταξύ τους.

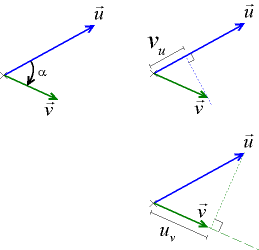
Προβολή διανύσματος σε διάνυσμα

Πρότυπο:ΔΜΟρισμός

Η προβολή ${\vec{α}}_{\vec{β}}$ είναι ομόρροπη του $\vec{β}$ , αν συν $(\hat{\vec{α}, \vec{β}})$ >0 και αντίρροπη, αν συν $(\hat{α, β})$ <0.

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Εικόνες	Λύση
	Αν συν $(\hat{\vec{α}, \vec{β}})$ >0, τότε η γωνία $(\hat{\vec{α}, \vec{β}})$ είναι οξεία. Η ορθή προβολή σημείου πλευράς οξείας γωνίας στην άλλη πλευρά ανήκει στην άλλη πλευρά. Επομένως, το πέρας της προβολής ${\vec{α}}_{\vec{β}}$ είναι στο ίδιο μέρος του πέρατος του $\vec{β}$ ως προς την αρχή του $\vec{β}$ , άρα ${\vec{α}}_{\vec{β}}$ είναι ομόρροπη του $\vec{b e t a}$ . Αν συν $(\hat{\vec{α}, \vec{β}})$ <0, τότε η γωνία $(\hat{\vec{α}, \vec{β}})$ είναι αμβλεία. Η ορθή προβολή σημείου πλευράς αμβλείας γωνίας στην άλλη πλευρά ανήκει στην προέκταση της άλλης πλευράς. Επομένως, το πέρας της προβολής ${\vec{α}}_{\vec{β}}$ είναι στο αντίθετο μέρος του πέρατος του $\vec{β}$ ως προς την αρχή του $\vec{β}$ , άρα ${\vec{α}}_{\vec{β}}$ είναι αντίρροπη του $\vec{β}$ .

Το μέτρο του ${\vec{α}}_{\vec{β}}$ είναι $| α | | σ υ ν (\hat{α, β})$ , αν και τα δύο διανύσματα είναι μη μηδενικά.

Άσκηση: Αποδείξτε ότι $\| {\vec{α}}_{\vec{β}} \| = \| α \| \| σ υ ν (\hat{\vec{α}, \vec{β}}) \|$
Εικόνα	Λύση
	Η αρχή και το πέρας του ${\vec{α}}_{\vec{β}}$ και η προβολή του πέρατος σχηματίζουν ορθογώνιο τρίγωνο, αν $\vec{α} \neq \vec{0}$ . Έστω η προσκείμενη γωνία του με κορυφή την αρχή θ. Εξ'ορισμού ισχύει ότι $σ υ ν θ = \frac{\| {\vec{α}}_{\vec{β}} \|}{\| α \|}$ . Η γωνία $(\hat{\vec{α}, \vec{β}})$ είναι είται ίση με θ ή παραπληρωματική σε αυτήν, σε κάθε περίπτωση ισχύει $σ υ ν (\hat{\vec{α}, \vec{β}}) = σ υ ν θ = \frac{\| {\vec{α}}_{\vec{β}} \|}{\| α \|} \Rightarrow \| {\vec{α}}_{\vec{β}} \| = \| α \| \| σ υ ν (\hat{\vec{α}, \vec{β}})$ .

Από τα δύο παραπάνω προκύπτει ότι ${\vec{α}}_{\vec{β}} = | \vec{α} | σ υ ν (\hat{\vec{α}, \vec{β}}) \hat{β} = | \vec{α} | σ υ ν (\hat{\vec{α}, \vec{β}}) \frac{\vec{β}}{| \vec{β |}} = \frac{| \vec{α} | | \vec{β} | σ υ ν (\hat{\vec{α}, \vec{β}})}{| \vec{β} |^{2}} \vec{β}$ . Η σχέση αυτή ισχύει και για $\vec{α} = \vec{0}$ , γιατί το μέτρο του μηδενικού διανύσματος είναι μηδέν. Επιπλέον, ισχύει ότι ${\vec{α}}_{\vec{β}} \cdot \vec{β} = \vec{α} \cdot \vec{β}$ , άρα το σύνολο των διανυσμάτων που έχουν κοινή αρχή με κάποιο διάνυσμα $\vec{β}$ και πέρας σε ευθεία κάθετη στο φορέα του $\vec{β}$ έχουν μεταξύ τους ίσα εσωτερικά γινόμενα.

Αν το διάνυσμα $\vec{β}$ είναι μοναδιαίο, τότε το εσωτερικό γινόμενο με οποιοδήποτε άλλο διάνυσμα παράγει το διάνυσμα προβολή κατά το φορέα του $\vec{β}$ . Για αυτό το λόγο τα μοναδιαία διανύσματα χρησιμοποιούνται γενικά ως φορείς κατεύθυνσης.

Αντίστροφα το εσωτερικό γινόμενο δύο μοναδιαίων διανυσμάτων αποδίδει τη σχέση των κατευθύνσεών τους, γιατί ισούται μόνο με το συνιμήτονο που λειτουργεί στο εσωτερικό γινόμενο ως δείκτης σχετικότητας κατευθύνσεων.

Εξωτερικό γινόμενο

Πρότυπο:ΔΜΟρισμός

Στον παραπάνω ορισμό το πρώτο διάνυσμα είναι το $\vec{α}$ και δεύτερο το $\vec{β}$ .

Απεικόνιση του εξωτερικού γινομένου (πράσσινο χρώμα) του μπλε με το κόκκινο διάνυσμα.

Το εξωτερικό γινόμενο εμφανίζεται συνήθως στην περιγραφή φαινομένων που αφορούν κάποια περιστροφή.

Ιδιότητες:

$\vec{α} \times \vec{β} = - \vec{β} \times \vec{α}$

Άσκηση: Αποδείξτε την παραπάνω πρόταση
Εικόνα	Λύση
	Έστω ότι και τα δύο διανύσματα είναι μη μηδενικά. Ισχύει ότι $\| \vec{α} \times \vec{β} \| = \| \vec{α} \| \| \vec{β} \| η μ ι (\hat{\vec{α}, \vec{β}}) = \| \vec{β} \| \| \vec{α} \| η μ ι (\hat{\vec{β}, \vec{α}} = \| \vec{β} \times \vec{α} \|)$ . Η διεύθυνση των δύο είναι η ίδια, κάθετα πάνω στο επίπεδο των $\vec{α}, \vec{β}$ . Σύφωνα με τον κανόνα του δεξιού χεριού τα δύο εξωτερικά γινόμενα είναι αντίρροπα. Επομένως, τα δύο εξωτερικά γινόμενα είναι αντίθετα. Στην περίπτωση που ένα από τα δύο είναι το μηδενικό διάνυσμα η σχέση γίνεται $\vec{0} = - \vec{0}$ που ισχύει.

$\vec{α} \times (\vec{β} \times \vec{γ}) = (\vec{α} \cdot \vec{γ}) \vec{β} - (\vec{α} \cdot \vec{β}) \vec{γ}$
$\vec{α} \times (\vec{β} + \vec{γ}) = \vec{α} \times \vec{β} + \vec{α} \times \vec{γ}$

Άρα και

(\vec{β} + \vec{γ}) \times \vec{α} = \vec{β} \times \vec{α} + \vec{γ} \times \vec{α}

$λ (\vec{α} \times \vec{β}) = (λ \vec{α}) \times \vec{β}$

Δύο διανύσματα μπορούν να ορίσουν πλήρως ένα τρίγωνο ή ένα παραλληλόγραμμο.

Άσκηση: Αποδείξτε την παραπάνω πρόταση
Τρίγωνο	Λύση	Παραλληλόγραμο
	Δύο διανύσματα με κοινή αρχή ορίζουν μια κυρτή γωνία και δύο ευθύγραμμα τμήματα στις πλευρές της, άρα και ένα τρίγωνο. Το άθροισμά τους προσδιορίζει και το τέταρτο σημείο ενός παραλληλογράμμου όπως αποδείχθηκε στην ενότητα της πρόσθεσης.

Το εμβαδόν του παραλληλογράμμου που ορίζεται από τα διανύσματα $\vec{α}$ , $\vec{β}$ ισούται με $| \vec{α} \times \vec{β} |$ .

Άσκηση: Αποδείξτε την παραπάνω πρόταση
Εικόνα	Λύση
	Το εμβαδόν παραλληλογράμμου ισούται με το μήκος της μίας πλευράς του επί το ύψος του. Αν θ η γωνία μεταξύ των δύο πλευρών, τότε το μήκος του ύψους ισούται με το ημθ επί το μήκος της άλλης πλευράς. Η γωνία θ σε παραλληλόγραμμο που ορίζεται από δύο διανύσματα ισούται με τη μεταξύ τους γωνία, άρα ισχύει το εμβαδόν ισούται με $\| \vec{α} \| \| \vec{β} \| η μ (\hat{\vec{α}, \vec{β}}) = \| \vec{α} \times \vec{β} \|$ .

Το εμβαδόν τριγώνου που ορίζεται από τα διανύσματα $\vec{α}$ , $\vec{β}$ ισούται με $\frac{1}{2} | \vec{α} \times \vec{β} |$ .

Άσκηση: Αποδείξτε την παραπάνω πρόταση
Εικόνα	Λύση
	Το εμβαδόν τριγώνου που ορίζεται από δύο διανύσματα ισούται με το μισό εμβαδόν παραλληλογράμμου που ορίζεται από δύο διανύσματα, γιατί ταυτίζεται με τρίγωνο που προκύπτει από το χωρισμό του παραλληλογράμμου από διαγώνιο του.

Το προσημασμένο εμβαδόν παραλληλογράμμου, τριγώνου, ή άλλου σχήματος μπορεί να αποκτήσει έννοια αν οριστεί φορά ροής στην περιφέρειά του. Ένα παράδειγμα που θα είχε έννοια είναι το εμβαδόν του ματιού ενός τυφώνα. Οι περιφέρειά του έχει κάποια ροή που το χαρακτηρίζει, την ροή του αέρα. Σε δύο τυφώνες που συγχωνέυονται το μάτι του τελικού τυφώνα θα έχει εμβαδόν που προσδιορίζεται ποιοτικά τουλάχιστον από το άθροισμα των προσημασμένων εμβαδών.

Mικτό γινόμενο

Πρότυπο:ΔΜΟρισμός

Ο όγκος παραλληλεπιπέδου που ορίζεται από τα διανύσματα $\vec{α}, \vec{β}, \vec{γ}$ είναι ίσος με $| \vec{α} \cdot (\vec{β} \times \vec{γ}) |$ .

Άσκηση: Αποδείξτε την παραπάνω πρόταση
εικόνα	Λύση
	Το εμβαδό της παραλληλόγραμμης βάσης $\vec{β}, \vec{γ}$ του παραλληλεπιπέδου ισούται με $\| \vec{β} \times \vec{γ} \|$ . Η διεύθυνση του $\vec{β} \times \vec{γ}$ είναι κάθετη στη βάση. Η φορά είναι είται προς το εσωτερικό του παραλληλεπιπέδου είται προς το εξωτερικό του. Το ύψος του παραλληλεπιπέδου ως προς αυτήν τη βάση είναι η προβολή ${\vec{α}}_{\vec{β} \times \vec{γ}}$ . Άρα ο όγκος ισούται με $\| {\vec{α}}_{\vec{β} \times \vec{γ}} \| \| \vec{β} \times \vec{γ} \| = \| {\vec{α}}_{\vec{β} \times \vec{γ}} \cdot \vec{β} \times \vec{γ} \| = \| \vec{α} \cdot (\vec{β} \times \vec{γ}) \|$

Ισχύει η ιδιότητα $\vec{α} \cdot (\vec{β} \times \vec{γ}) = (\vec{α} \times \vec{β}) \cdot \vec{γ}$ .

Παραλληλία

Δύο μη μηδενικά διανύσματα είναι παράλληλα αν και μόνο αν $\vec{α} \times \vec{β} = \vec{0}$ .

Άσκηση: Αποδείξτε τη συνθήκη παραλληλίας
Λύση
Από τον ορισμό του εξωτερικού γινομένου για μη μηδενικά διανύσματα προκύπτει ότι δύο διανύσματα έχουν εξωτερικό γινόμενο μηδέν αν και μόνο αν η μεταξύ τους γωνία είναι 0 ή π ακτίνια, δηλαδή είναι ομόρροπα ή αντίρροπα μεταξύ τους. Σε κάθε περίπτωση είναι παράλληλα.

Ισχύει η σχέση $\vec{α} \times \vec{β} = \vec{0} \Leftrightarrow \vec{α} = \vec{0} \overset{´}{η} \vec{β} = \vec{0} \overset{´}{η}$ τα δύο διανύσματα είναι παράλληλα μεταξύ τους.

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Λύση
Δύο διανύσματα είναι και τα δύο μηδενικά ή δεν είναι και τα δύο μηδενικά. Αν δεν είναι και τα δύο μηδενικά τότε ισχύει η συνθήκη παραλληλίας, αλλιώς τουλάχιστον ένα είναι το μηδενικό διάνυσμα.

Διαίρεση διανυσμάτων

Δεν υπάρχει ευρέως αποδεκτή διαίρεση διανυσμάτων, εκτός ίσως από τον όρο $\frac{α}{β}$ που συναντήσαμε στο βαθμωτό πολλαπλασιασμό, γιατί δεν υπάρχει ουδέτερη κατεύθυνση. Η επίλυση εξισώσεων που στηρίζεται αλγεβρικά σε διαίρεση γίνεται μόνο και με τα δύο είδη πολλαπλασιασμών διανυσμάτων.

Αν $\vec{α}, \vec{β}, \vec{γ}$ μη μηδενικά διανύσματα τότε ισχύουν οι εξής ισοδυναμίες:

$\vec{α} \times \vec{δ} = \vec{0}$ και $\vec{α} \cdot \vec{δ} = \vec{0} \Leftrightarrow \vec{δ} = \vec{0}$

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Εικόνα	Λύση
Οπτικοποίηση των δύο γινομένων. Αν και τα δύο εμβαδά είναι μηδέν υποχρεωτικά ένα διάνυσμα είναι μηδενικό, δηλαδή σημείο.	Αν δεν είναι μηδενικό το διάνυσμα, τότε ισχύουν ταυτόχρονα οι συνθήκες παραλληλίας και καθετότητας που είναι άτοπο.

$\vec{α} \times \vec{β} = \vec{α} \times \vec{γ}$ και $\vec{α} \cdot \vec{β} = \vec{α} \cdot \vec{γ} \Leftrightarrow \vec{β} = \vec{γ}$

Άσκηση: Αποδείξτε την παραπάνω ιδιότητα
Λύση
$\vec{α} \times \vec{β} = \vec{α} \times \vec{γ}$ και $\vec{α} \cdot \vec{β} = \vec{α} \cdot \vec{γ} \Leftrightarrow$ $\Leftrightarrow \vec{α} \times (\vec{β} - \vec{γ}) = \vec{0}$ και $\vec{α} \cdot (\vec{β} - \vec{γ}) = \vec{0} \Leftrightarrow \vec{β} - \vec{γ} = \vec{0} \Leftrightarrow \vec{β} = \vec{γ}$

Δύναμη διανύσματος

Πρότυπο:ΔΜΟρισμός

Ισχύει ότι ${\vec{α}}^{2} = | \vec{α} |^{2}$ .

Άσκηση: Αποδείξτε ότι ${\vec{α}}^{2} = \| \vec{α} \|^{2}$
Λύση
${\vec{α}}^{2} = \| \vec{α} \| \| \vec{α} \| σ υ ν (\hat{\vec{α}, \vec{α}}) = \| \vec{α} \|^{2}$ , αφού συν $(\hat{\vec{α}, \vec{α}})$ =συν0=1.

Ασκήσεις

(Προσοχή στις ερωτήσεις-παγίδες!)

Ερωτήσεις κατανόησης

Ισχύει η προσεταιριστική ιδιότητα στο διπλό εσωτερικό γινόμενο $\vec{α} \cdot \vec{β} \cdot \vec{γ}$ ; Η αντιμεταθετική;

Απάντηση
Δεν υπάρχει διπλό εσωτερικό γινόμενο! Ισχύει ότι $\vec{α} \cdot \vec{β} \cdot \vec{γ} = (\vec{α} \cdot \vec{β}) \vec{γ}$ που είναι διάνυσμα, αφού ο παράγοντας $\vec{α} \cdot \vec{β}$ είναι αριθμός.
Επερώτηση: Ποιοί πολλαπλασιασμοί υπάρχουν σε αυτή τη μορφή;

Μπορείτε να εφαρμόσετε τον κανόνα του δεξιού χεριού σε αντίθετα και ομόρροπα διανύσματα;
Γιατί τρία μη συνευθειακά διανύσματα ορίζουν παραλληλεπίπεδο; Ποιά η συνθήκη ισοδυναμίας, ώστε αυτό το παραλληλεπίπεδο είναι ορθογώνιο;
Τί ιδιότητες έχει το διάνυσμα $\vec{α} \times (\vec{β} \cdot \vec{γ})$ ;
Ποιό διάνυσμα είναι το $\vec{α} \times \vec{α}$ ; Γιατί δεν ορίστηκε έτσι το τετράγωνο διανύσματος;

Απάντηση
Ισχύει $\vec{α} \times \vec{α} = \vec{0}$ για κάθε $\vec{α}$ . Το τετράγωνο διανύσματος δεν ορίστηκε έτσι, γιατί δεν έχει νόημα να οριστεί μια πράξη της οποίας το αποτέλεσμα είναι μοναδικό.
Επερώτηση: Γιατί το τετράγωνο διανύσματος δεν ορίστηκε με βάση το βαθμωτό πολλαπλασιασμό;

Αποδεικτικές ασκήσεις

Αποδείξτε την ιδιότητα $(\vec{α} + \vec{δ}) \cdot (\vec{β} + \vec{γ}) = \vec{α} \cdot \vec{β} + \vec{α} \cdot \vec{γ} + \vec{δ} \cdot \vec{β} + \vec{δ} \cdot \vec{γ}$ .
Αποδείξτε την ιδιότητα $(λ \vec{α}) \cdot (μ \vec{β}) = (λ μ) (\vec{α} \cdot \vec{β})$
Βρείτε τη συνθήκη ομορροπίας και ετεροποίας σε αλγεβρική διανυσματική μορφή. Ύστερα συνδέστε την με τη συνθήκη παραλληλίας.
Αποδείξτε ότι ${\vec{α}}_{\vec{β}} = \vec{α} \cdot \hat{β} \hat{β} .$
Αποδείξτε ότι (α→⋅β→)2+(α→×β→)2=α→2β→2
- Σε ποιά ταυτότητα στηριχθήκατε για την παραπάνω απόδειξη;
Ποιές αλγεβρικές ταυτότητες ισχύουν αντίστοιχα στην αναλυτική γεωμετρία; Αυτές που δε λειτουργούν πώς μπορούν να διορθωθούν ώστε να λειτουργούν;

Ερευνητικά θέματα

Μπορείται να γενικεύσετε τον ορισμό του μεικτού γινομένου ως προς τη λειτουργικότητά του στις ν διαστάσεις;

Πράξεις διανυσμάτων\Μέρος Β

Περιεχόμενα